
Algoritmi sortiranja prestavljaju algoritme čiji je cilj da postave elemente kolekcije u ispravan redosled. Najčešće se redosled utvrđuje operatorom poređenja koji se definiše za elemente. Kod brojnih vrednosti to može biti operator < ili >, tekstualne tipove možemo sortirati leksikografski (u abedecnom redosledu) ili po dužini podatka…
Sortiranje se primenjuje kako bi podaci bili pregledniji, odnosno kako bi se lakše pretraživali. Takođe, sortiranje može da olakša i uprosti izvršavanje narednih operacija.
Pominju se uvek u množini (“algoritmi sortiranja”), što sugeriše da ne postoji jedan najbolji za svaku kolekciju već je, spram konteksta, potrebno izabrati onaj koji najbolje odgovara.
Neki algoritmi sortiranja omogućuju “in-place” implementaciju (imlementaciju “u mestu”). Ona podrazumeva da se ispravan redosled elemenata postiže zamenom mesta elemenata u okviru iste memorijske strukture, bez potrebe za zauzimanjem dodatnim memorijski lokacija. Benefiti ove osobine posebno dolaze do izražaja kada je memorijski prostor ograničen.
Što se tiče vremenske kompleksnosti, prepoznaju se dve klase algoritama – algoritmi sa kvadratnom složenošću O(n^2) i algoritmi sa O(n log n) složenošću.
Algoritmi sa O(n^2) složenošću
U ovu grupu “manje efikasnih” algoritama spadaju selection sort, bubble sort i insertion sort. Intuitivni su, lako razumljivi i jednostavni za prvo samostalno implementiranje. Međutim, njihovi nedostaci dolaze do izražaja kada se broj elemenata poveća. Kada se broj elemenata udesetostruči, broj operacija (što se relativno direktno može mapirati i na vreme izvršavanja) se povećava 100 puta. Ne zvuči sjajno, zar ne? Na slici možemo videti vreme izvršavanja (u sekundama) ova tri algoritma nad kolekcijom od 100, 1000, 10 000 i 100 000 elemenata.
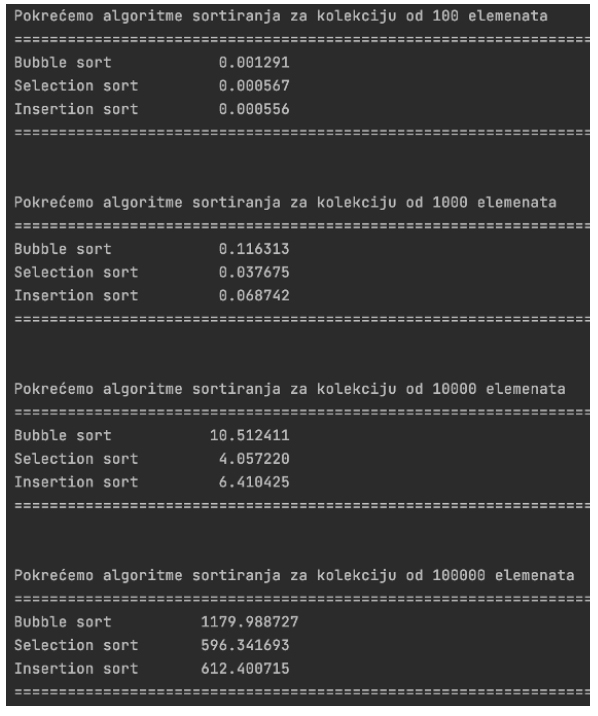
Algoritmi sa O(n log n) složenošću
Glavni predstavnici ove grupe su merge sort, heap sort i timsort. U ovu grupu se često uvrštava i quick sort. Quick sort je specifičan po tome što se, ako posmatramo zaista najgori slučaj (što veliko O notacija analizira), izvršava u O(n^2). Međutim, statistički, šanse da se taj najgori slučaj i ostvari u praksi su jako male. Zato kažemo da se, u prosečnom slučaju, quick sort izvršava u O(n log n).
Koliko su ovi algoritmi efikasniji, pogotovo na kolekcijama sa velikim brojem elemenata možemo videti na prilikom eksperimentalnog pokretanja nad kolekcijama od 100, 1000, 10 000 i 100 000 elemenata.
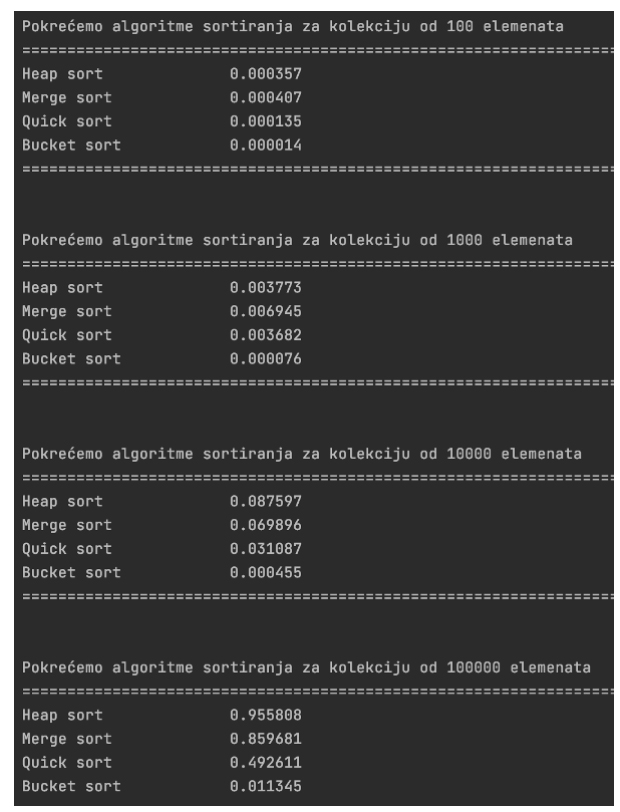
Kada uporedimo vremena izvršavanja algoritama iz naše dve klase, videćemo da se ne razlikuju previše kada je broj elemenata kolekcije mali. Međutim, kada se broj elemenata drastično poveća, razlike postaju ogromne. Sortiranje kolekcije od 100 000 elemenata traje oko 600 sekundi za algoritam sa O(n^2) u odnosu na ispod sekunde za O(n log n).

