U ovom postu nastavljamo priču o čuvenoj Big O (veliko O) notaciji. Ukoliko niste pročitali prethodni post sa naslovom “Algoritmi za početnike: Procena vremenske kompleksnosti“ započnite čitanje odatle.
Ako na Google pretraživaču unesete „Veliko O notacija” prvi pogodak je članak sa Wikipedije https://sr.wikipedia.org/sr-ec/Велико_О. Bez upozorenja „samo za najhrabrije“ i „ulazite na sopstvenu odgovornost“ programer početnik bi lako mogao da dođe do zaključka da veliko O notacija jednostavno nije za njega, da je strašna i komplikovana. Nije baš tako.
Veliko O notacija govori o vremenskoj kompleksnosti odnosno o broju operacija potrebnih da se algoritam izvrši u najgorem slučaju. Dakle, veliko O notacija zanemaruje faktor hardvera (jer ne procenjuje vreme nego broj operacija) kao i faktor sreće jer analizira najgori mogući slučaj.
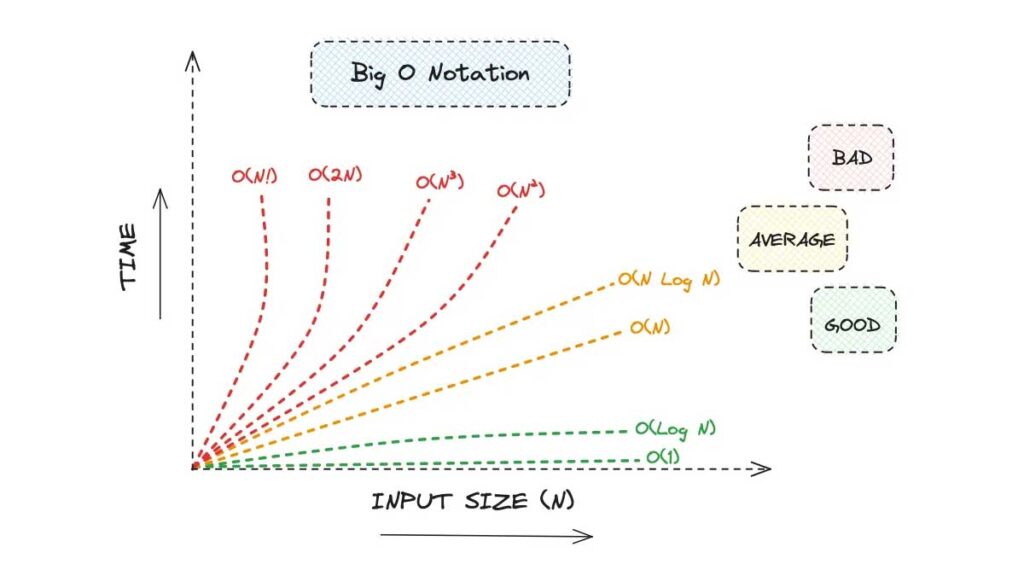
Karakteristične kompleksnosti su (u rastućem redosledu, od najbolje do najgore):
O(1) – konstantno vreme. Ukoliko algoritam ima ovu kompleksnost znači da vreme izvršavanje ne zavisi od veličine ulaznih podataka.
O(log n) – logaritamsko vreme. Ko se još seća logaritama? Kod algoritama sa ovom kompleksnošću za povećanje veličine ulaza na kvadrat, vreme izvršavanja (odnosno broj operacija) se povećava svega 2 puta. Primer algoritma sa ovom kompleksnošću je binarna pretraga.
O(n) – linearno vreme. Kod algoritama sa ovom kompleksnošću za povećanje veličine ulaza 10 puta i vreme izvršavanja (odnosno broj operacija) se povećava 10 puta. Primer algoritama sa ovom kompleksnošću su algoritmi minimuma i maksimuma, sumiranje elemenata niza, traženje elemenata u nizu..
O(n log n) – n log n vreme. Algoritmi sa ovom kompleksnošću su “efikasniji” algoritmi sortiranja poput merge sort-a i quick sort-a.
O(n^2) – kvadratno vreme. Kod algoritama sa ovom kompleksnošću za povećanje veličine ulaza 10 puta vreme izvršavanja (odnosno broj operacija) se povećava kvadratno, dakle 100 puta. Ova kompleksnost se javlja kod nekih algoritama sortiranja (selection sort, insertion sort).
U prethodnom postu smo objasnili kako da procenimo okviran broj operacija potreban za izvršavanje nekog algoritma. Nastavićemo od zaključka da je za algoritam maksimuma od n elemenata potrebno 3*n+2 operacije. Međutim, kod karakterističnih kompleksnosti vidimo da se ništa slično ne pojavljuje. Zašto je to tako?
Razlog je zato što veliko O notacija predstavlja procenu kompleksnosti i obuhvata nekoliko aproksimacija. Kod funkcije 3*n+2 ova konstanta 2 nema prevelik uticaj na rast vrednosti s obzirom da je n najveći stepen polinoma (šta ono beše polinom?) i diktira rast. Kada određujemo kompleksnost programa koji ima polinomijalni broj operacija (recimo 10n^4-3n^3+2n^2+n+3) uzima se u obzir samo najveći stepen polinoma dakle 10n^4, ostali imaju manju uticaj pa se mogu zanemariti.
Drugo pravilo kaže da se i konstante mogu zanemariti. Dakle, 10n^4 je isto što i n^4.
Da sumiramo, ukoliko procenimo da naš program ima 10n^4-3n^3+2n^2+n+3 operacija, njegova vremenska kompleksnost je O(n^4). Ova kompleksnost je relativno retka u računarstvu, ali ovde nam je poslužila kao primer.
Ako se vratimo na primer sa algoritmom maksimuma za 3*n+2 operacija određujemo da je kompleksnost linearna odnosno O(n).
Naravno, kada se uvežbate u proceni kompleksnosti, neće biti potrebno da brojite svaku pojedinačnu operaciju nego ćete moći ove aproksimacije da izračunate “iz glave”
Ukoliko vam ipak treba pomoć, sajt https://www.bigocalc.com može časkom izračunati kompleksnost vašeg segmenta koda.

